Answer:
The correct options are B and C.
Explanation:
Graph A represents the parent quadratic function.

The vertex from of a parabola is

where, (h,k) is vertex and a is a constant.
If |a|>1, then parent function is stretched by factor a and If 0<|a|<1, then parent function is compressed by factor a.
The vertex of graph B is at (1,0). So the function of graph B is
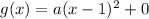
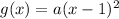
Graph B passes through (3,0), so
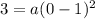
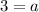
The value of a is 3. So, the function of graph B is
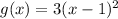
If means the graph A stretched vertically by factor 3 and translate 1 unit to the right.
Therefore the correct options are B and C.