Answer:
It is a solution
Explanation:
Check and see if (0,0) satisfies both inequalities.
The first inequality is:
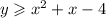
When we put x=0, and y=0, we get:
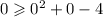
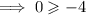
This part is true.
The second inequality is:
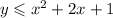
We put x=0 and y=0 to get:
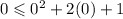
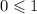
This part is also true.
Since the (0,0) not satisfy both, inequalities, it is a solution.