Final Answer:
On a hot day, the center of the railroad rail would rise approximately 8 millimeters above the ground.
Step-by-step explanation:
The expansion of the railroad rail can be calculated using the formula:
![\[ \text{Expansion} = \text{Coefficient of Expansion} * \text{Original Length} * \text{Change in Temperature} \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/q5b2ww498u3jua9s5w96jl9ebpqxtcollk.png)
In this case, the coefficient of linear expansion for steel (commonly used for railroad rails) is approximately
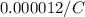 , the original length of the rail is 4 kilometers (or 4000 meters), and the change in temperature is the equivalent of 16 centimeters (or 0.16 meters). Plugging these values into the formula:
, the original length of the rail is 4 kilometers (or 4000 meters), and the change in temperature is the equivalent of 16 centimeters (or 0.16 meters). Plugging these values into the formula:
![\[ \text{Expansion} = 0.000012 * 4000 * 0.16 \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4dxjevgqklbxyp44n4h8dbckrwhx8sghct.png)
![\[ \text{Expansion} = 0.768 \, meters \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/khu98fd8rrlp3ftv560101lv7iupnluhn6.png)
This is the total expansion of the rail. However, we are interested in the rise of the center, which is half of the total expansion. Therefore, the rise of the center is:
![\[ \text{Rise of Center} = 0.5 * 0.768 \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wvari7jzwf3j4vjmu1txxskmmdkdoy5p0d.png)
![\[ \text{Rise of Center} = 0.384 \, meters \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/cd2850nfxzyqzkjsfl280cw4lp8k4alnzn.png)
To convert this into millimeters, we multiply by 1000:
![\[ \text{Rise of Center} = 384 \, millimeters \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/u7mnb8xi8s1vu9e3xrgcm3fr55z4p4qsp4.png)
So, on a hot day, the center of the railroad rail would rise approximately 8 millimeters above the ground. This expansion due to temperature changes is crucial to consider in engineering and construction to prevent issues such as buckling or warping of materials.