Answer:
D.
Explanation:
You could find the 8 terms and then add them up.
Let's do that.
Luckily we have the common ratio which is -5. Common ratio means it is telling us what we are multiplying over and over to get the next term.
The first term is -11.
The second term is -5(-11)=55.
The third term is -5(55)=-275.
The fourth term is -5(-275)=1375.
The fifth term is -5(1375)=-6875.
The sixth term is -5(-6875)=34375.
The seventh terms is -5(34375)=-171875.
The eighth term is -5(-171875)=859375.
We get add these now. (That is what sum means.)
-11+55+-275+1375+-6875+34375+-171875+859375
=716144 which is choice D.
Now there is also a formula.
If you have a geometric series, where each term of the series is in the form
 , then you can use the following formula to compute it's sum (if it is finite):
, then you can use the following formula to compute it's sum (if it is finite):
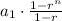
where
 is the first term and
is the first term and
 is the common ratio. n is the number of terms you are adding.
is the common ratio. n is the number of terms you are adding.
We have all of those. Let's plug them in:
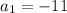 ,
,
 , and
, and
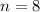
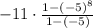

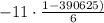

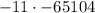
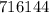
Either way you go, you should get the same answer.