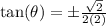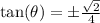Question

If sine theta equals one over three, what are the values of cos θ and tan θ?

cosine theta equals plus or minus four over three, tangent theta equals plus or minus one over two
cosine theta equals plus or minus two times square root of two over three, tangent theta equals plus or minus square root of two over four
cosine theta equals plus or minus four over three, tangent theta equals negative one over two
cosine theta equals plus or minus two times square root of two over three, tangent theta equals negative square root of two over two

Answer 1

So second choice.

`\cos(\theta)=\pm (2√(2))/(3)`

`\tan(\theta)=\pm (√(2))/(4)`

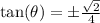
Explanation:

I'm going to use a Pythagorean Identity, name the one that says:

`\sin^2(\theta)+\cos^2(\theta)=1`.

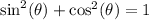We are given:
`\sin(\theta)=(1)/(3)`.

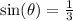Inserting this into our identity above gives us:

`((1)/(3))^2+\cos^2(\theta)=1`

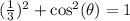
Time to solve this for the cosine value:

`(1)/(9)+\cos^2(\theta)=1`

Subtract 1/9 on both sides:

`\cos^2(\theta)=1-(1)/(9)`

`\cos^2(\theta)=(8)/(9)`

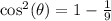
Square root both sides:

`\cos(\theta)=\pm \sqrt{(8)/(9)}`

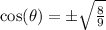
9 is a perfect square but 8 is not.

8 does contain a factor that is a perfect square which is 4.

So time for a rewrite:

`\cos(\theta)=\pm (√(4)√(2))/(3)`

`\cos(\theta)=\pm (2√(2))/(3)`

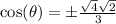
So without any other give information we can't know if cosine is positive or negative.

Now time for the tangent value.

You can find tangent value by using a quotient identity:

`\tan(\theta)=(\sin(\theta))/(\cos(\theta))`

`\tan(\theta)= ((1)/(3))/(\pm (2√(2))/(3))`

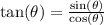
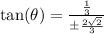
Multiply top and bottom by 3 get's rid of the 3's on the bottom of each mini-fraction:

`\tan(\theta)=\pm (1)/(2 √(2))`

Multiply top and bottom by sqrt(2) to get rid of the square root on bottom:

`\tan(\theta)=\pm (1(√(2)))/(2√(2)(√(2)))`

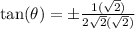
Simplifying:

`\tan(\theta)=\pm (√(2))/(2(2))`

`\tan(\theta)=\pm (√(2))/(4)`

Answer 2

cosine theta equals plus or minus two times square root of two over three, tangent theta equals plus or minus square root of two over four

Explanation:

Given:

sinθ=1/3

θ=19.47 degrees

then

cosθ= cos(19.47)=0.942 = 2(√2/3)

tanθ=tan(19.47)=0.35= √2/4

Hence option two is correct:cosine theta equals plus or minus two times square root of two over three, tangent theta equals plus or minus square root of two over four!