Answer:
The resulting pressure after the reaction occurs is 13,333.3333 kPa
Step-by-step explanation:
The combined gas law for an ideal gas is:

Where,
P₁ , V₁ , n₁ , T₁ are the pressure, volume, moles and temperature respectively of ideal gas 1.
P₂ , V₂ , n₂ , T₂ are the pressure, volume, moles and temperature respectively of ideal gas 2.
For the question, temperature stays constant and the volume ("closed chamber") are constant.
Thus, equation using for the question:
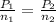
On the reactant side, number of moles = 2 + 1 = 3 moles
On the product side, number of moles = 2 moles
Given: P₁ = 20,000 kPa
Substituting the values and solving for P₂ gives
20,000kPa / 3 = P₂/2
P₂ = 13,333.3333 kPa