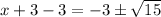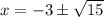Question

Solve by completing the square. x2+6x−6=0

Answer 1

`x=-3\±√(15)`

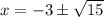
Explanation:

We have the following equation

`x^2+6x-6=0`

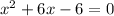
To use the method of completing squares you must take the coefficient of x and divide it by 2 and square the result.

`((6)/(2))^2=9`

Now add 9 on both sides of equality

`(x^2+6x+ 9)-6=9`

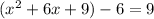
Factor the term in parentheses

`(x+3)^2-6=9`

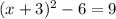
Add 6 on both sides of the equation

`(x+3)^2-6+6=9+6`

`(x+3)^2=15`

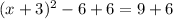
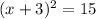
Take square root on both sides of the equation

`√((x+3)^2)=\±√(15)`

`x+3=\±√(15)`

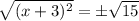
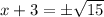
Subtract 3 from both sides of the equation.

`x+3-3=-3\±√(15)`

`x=-3\±√(15)`

Answer 2

For this case we must solve the following equation by completing squares:

`x ^ 2 + 6x-6 = 0`

We add 6 to both sides of the equation:

`x ^ 2 + 6x = 6`

We divide the middle term by 2, and square it:

`(\frac {6} {2}) ^ 2`

And we add it to both sides of the equation:

`x ^ 2 + 6x + (\frac {6} {2}) ^ 2 = 6 + (\frac {6} {2}) ^ 2\\x ^ 2 + 6x + (3) ^ 2 = 6 + 9`

We rewrite the left part of the equation:

`(x + 3) ^ 2 = 15`

We apply root to both sides:

`x + 3 = \pm \sqrt {15}`

We have two solutions:

`x_ {1} = \sqrt {15} -3\\x_ {2} = - \sqrt {15} -3`

Answer:

`x_ {1} = \sqrt {15} -3\\x_ {2} = - \sqrt {15} -3`