Answer:
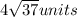 is the perimeter of square ABCD.
is the perimeter of square ABCD.
Explanation:
Coordinates of square ABCD:
A = (3,4), B = (2,-2), C = (-4-1) , D = (-3,5)
Distance formula:
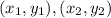
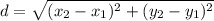
Distance of AB: A = (3,4), B = (2,-2)
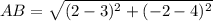
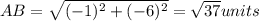
Given that the ABCD is square, then:
AB = BC = CD = DA
Perimeter of the square ABC = AB +BC + CD + DA
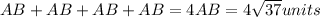
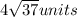 is the perimeter of square ABCD.
is the perimeter of square ABCD.