Answer:
Option b Tyree’s solution is inaccurate. In step 1, he substituted incorrectly.
Explanation:
we know that
the formula to calculate the distance between two points is equal to

we have
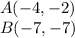
step 1
substitute the values in the formula

step 2
Simplify
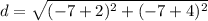
step 3
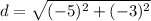
step 4
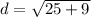
step 5
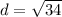
therefore
Tyree’s solution is inaccurate. In step 1, he substituted incorrectly.