F(x) = -x^3 + 3x^2 + x - 3 Using the end behavior of f(x), determine the graph of the function

Question

asked Feb 19, 2020 135k views

2 Answers

Phiter · Answer 1 · 2020-02-25T20:24:35+0000

Answer:

Here, the given function,

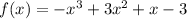
f(x) = -x^3 + 3x^2 + x - 3

Since, the leading coefficient is negative, and degree is odd,

Thus, the end behaviour of the function is,

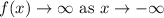
$f(x)\rightarrow \infty\text{ as }x\rightarrow -\infty$

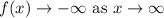
$f(x)\rightarrow -\infty\text{ as }x\rightarrow \infty$

Therefore, the graph rises to the left and falls to the right.

Now, when f(x) = 0

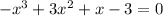
-x^3+3x^2+x-3=0

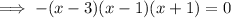
$\implies -(x-3)(x-1)(x+1)=0$

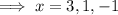
$\implies x=3, 1, -1$

That is, graph intercepts the x-axis at (3, 0), (1, 0) and (-1, 0).

When x = 0,

f(x) = - 3

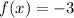
That is, graph intersects the y-axis at ( 0, -3),

Also, for 0 > x > -1 , f(x) is decreasing,

For 2.55 > x > 0, f(x) is increasing,

For 3 > x > 2.55, f(x) is decreasing,

Hence, by the above explanation we can plot the graph of the function ( shown below )