Answer:
The correct option is D.
Explanation:
Consider the provided expression.
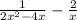
Now take the LCM of the denominator and solve the above expression as shown:
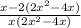
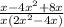
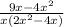
Cancel out the x as it is common in numerator and denominator.
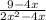
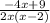
Hence, the correct option is D.