Question

Consider the table of values for function f.

x: -1, 0, 1, 2, 3, 4, 5
f(x): 3.5, 4, 5, 7, 11, 19, 35

The function g is shown below:

g(x)=4x+5

In which of the following intervals is the average rate of change greater for f than for g?

A. [1,3]
B. [3,5]
C. [0,2]
D. [-1,0]

Answer 1

B. [3,5]

Explanation:

The rate of change of a function is the same as the slope between two given points from that same function,

Hence,

all we need to do is use the slope's equation, that is

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

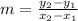
And eval it in every couple of ordered pairs given from the table we obtain the following>

x2 y2 x1 y1 m

0 4 -1 3,5 0,5

1 5 0 4 1

2 7 1 5 2

3 11 2 7 4

4 19 3 11 8

5 35 4 19 16

The rate of change from g(x) is 4 (its slope)

Hence, the interval when the rate of change of f(x) is greater than g(x) is from x=3 to x=5