Step-by-step explanation:
It is given that,
Speed of the electron in horizontal region,
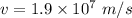
Vertical force,
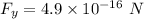
Vertical acceleration,
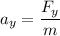
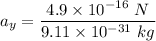
 ..........(1)
..........(1)
Let t is the time taken by the electron, such that,
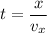

 ...........(2)
...........(2)
Let
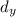 is the vertical distance deflected during this time. It can be calculated using second equation of motion:
is the vertical distance deflected during this time. It can be calculated using second equation of motion:
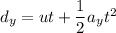
u = 0
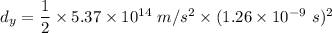
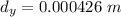
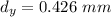
So, the vertical distance the electron is deflected during the time is 0.426 mm. Hence, this is the required solution.