Answer : The partial pressure of
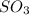 is, 67.009 atm
is, 67.009 atm
Solution : Given,
Partial pressure of
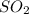 at equilibrium = 30.6 atm
at equilibrium = 30.6 atm
Partial pressure of
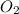 at equilibrium = 13.9 atm
at equilibrium = 13.9 atm
Equilibrium constant =
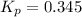
The given balanced equilibrium reaction is,
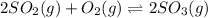
The expression of
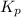 will be,
will be,
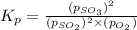
Now put all the values of partial pressure, we get
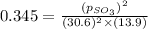
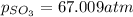
Therefore, the partial pressure of
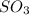 is, 67.009 atm
is, 67.009 atm