Question

In January 2002, two students made worldwide headlines by spinning a Belgian euro 250 times and getting 140 heads—that’s 56%. That makes the 90% confidence interval (51%, 61%). What does this mean? Are these conclusions correct? Explain.

Answer 1

Answer with explanation:

The 90% confidence interval (51%, 61%) for proportion means that the proportion of getting heads lie in it.

Given : Total number of times coin is tossed = 250

Number of times they got head =140

The probability of getting a head = 0.56

The confidence interval for proportion is given by :-

`p\pm z_(\alpha/2)\sqrt{(p(1-p))/(n)}`

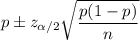
Given significance level :
`\alpha=1-0.90=0.1`

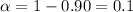
Critical value :
`z_(\alpha/2)=z_(0.05)=\pm1.645`

Now, the 90​% confidence interval for proportion will be :-

`0.56\pm (1.645)\sqrt{(0.56(1-0.56))/(250)}\approx0.56\pm 0.0516\\\\=(0.56-0.0516,0.56+0.0516)=(0.5084,\ 0.6116)\approx(51\%,\ 61\%)`

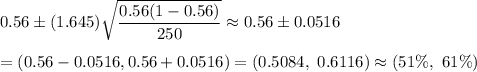
Hence, the given confidence interval is correct.