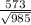Question

Find the rate of change of f(x,y,z)=xyzf(x,y,z)=xyz in the direction normal to the surface yx2+xy2+yz2=120yx2+xy2+yz2=120 at (3,4,3)(3,4,3). (Use symbolic notation and fractions where needed.) Rate of change =

Answer 1

Rate of change of function in the direction of normal to the given surface at ( 3 , 4 , 3 ) is
`(573)/(√(985))`

Explanation:

Given:

Function, f( x , y , z ) = xyz

Equation of surface, yx² + xy² + yz² = 120

To find: Rate of change of function in the direction of normal to the given surface at ( 3 , 4 , 3 )

The Gradient of the normal to the surface

`(\bigtriangledown_x\:,\:\bigtriangledown_y\:,\:\bigtriangledown_z)`

`\implies\:(2xy+y^2+0\:,\:x^2+2xy+z^2\:,\:0+0+2zy)`

`\implies\:(2xy+y^2\:,\:x^2+2xy+z^2\:,\:2zy)`

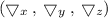
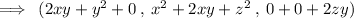
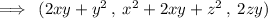
Gradient at ( 3 , 4 , 3 )
`=\:(2(3)(4)+(4)^2\:,\:(3)^2+2(3)(4)+(3)^2\:,\:2(4)(3))`

`\implies\:(40\:,\:42\:,\:24)`

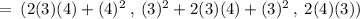
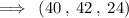
The Change in the directional derivative of f in given direction is,

`\bigtriangledown f_((3,4,3)).((40,42,24))/(√(40^2+42^2+24^2))=(yz,xz,xy)_((3,4,3)).((40,42,24))/(√(1600+1764+576))=((4)(3),(3)(3),(3)(4)).((40,42,24))/(√(3940))`

`=((12,9,12).(40,42,24))/(√(3940))=(480+378+288)/(√(3940))=(1146)/(2√(985))=(573)/(√(985))`

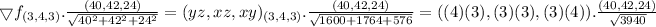
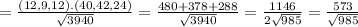
Therefore, Rate of change of function in the direction of normal to the given surface at ( 3 , 4 , 3 ) is
`(573)/(√(985))`