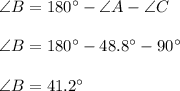Question

Please help soon. Solve the right triangle shown in the figure.

Answer 1

Answer: option c.

Explanation:

To find AB you can use this trigonometric identity:

`tan\alpha=(opposite)/(adjacent)`

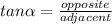
In this case:

`\alpha=\angle A=48.8\°\\opposite=BC=1.6in\\adjacent=AC`

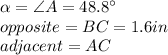
Substituting values and solving for AC, we get:

`tan(48.8\°)=(1.6in)/(AC)\\\\AC=(1.6in)/(tan(48.8\°))\\\\AC=1.4in`

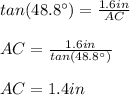
To find AB you can use the Pythagorean Theorem:

`c^2=a^2+b^2`

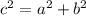
Where "c" is the hypotenuse and "a" and "b" are the legs of the triangle.

In this case:

`c=AB\\b=AC=1.4in\\\\a=BC=1.6in`

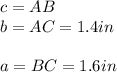
Substituting values and solving for AB, we get:

`AB^2=(1.6in)^2+(1.4in)^2\\\\AB=√((1.6in)^2+(1.4in)^2)\\\\AB=2.1in`

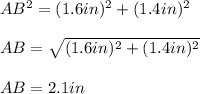
Since the sum of the interior angles of a triangle is 180 degrees, we know that ∠B is:

`\angle B=180\°-\angle A-\angle C\\\\\angle B=180\°-48.8\°-90\°\\\\\angle B=41.2\°`