Question

Sara wanted to gather data about the cost of local gyms in her area. She plotted the data and determined that the average gym costs consist of a one-time registration fee and a monthly fee modeled by the equation y = 10x + 30.

Identify and interpret the y-intercept in this model.

a. The y-intercept is 30. This is the cost of registration.
b. The y-intercept is 30. This is the cost per month.
c. The y-intercept is 10. This is the cost of registration.
d. The y-intercept is 10. This is the cost per month.

Answer 1

`\bf y = \stackrel{\stackrel{monthly~fee}{\downarrow} }{10}~~\stackrel{\stackrel{month}{\downarrow }}{x}+\underset{y-intercept}{\stackrel{\stackrel{registration~fee}{\downarrow }}{30}}~\hfill \impliedby \begin{array} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}`

Answer 2

Answer: a. The y-intercept is 30. This is the cost of registration.

Explanation:

The standard equation of line in intercept form is given by :-

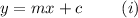`y=mx+c\ \ \ \ \ \ \ (i)`, where m is the slope of the line and c is the y-intercept.

Given : Sara plotted the data and determined that the average gym costs consist of a one-time registration fee and a monthly fee modeled by the equation :-

`y = 10x + 30`

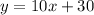
By comparing it to the equation (i), we have

c=30 and m=10

i.e. The y-intercept is 30.

Also, y-intercept of any function shows the starting value of the function when x=0.

Thus, This is the cost of registration ( starting fee).