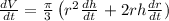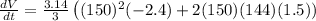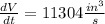Question

The radius of a right circular cone is increasing at a rate of 1.5 in/s while its height is decreasing at a rate of 2.4 in/s. At what rate is the volume of the cone changing when the radius is 150 in. and the height is 144 in.?

Answer 1

`11304 (in^(3))/(s)`

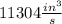
Step-by-step explanation:

r = radius of right circular cone = 150 in

h = height of right circular cone = 144 in

`(dr)/(dt)` = rate at which radius increase = 1.5 in/s

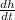`(dh)/(dt)` = rate at which height decrease = - 2.4 in/s

Volume of the right circular cone is given as

`V = (\pi r^(2)h)/(3)`

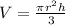
Taking derivative both side relative to "t"

`(dV)/(dt) = (\pi )/(3)\left ( r^(2)(dh)/(dt) \right + 2rh(dr)/(dt))`

`(dV)/(dt) = (3.14 )/(3)\left ( (150)^(2)(- 2.4) + 2(150)(144)(1.5))`

`(dV)/(dt) = 11304 (in^(3))/(s)`