Question

Find the discriminant and the numbers of real roots for this equation: 4x^2+12x+9=0

Answer 1

Answer: 0; one real number

Explanation:

Answer 2

`D=0`

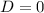
The quadratic equation has one real root with a multiplicity of 2.

Explanation:

Given a quadratic equation:

`ax^2+bx+c=0`

You can find the Discriminant with this formula:

`D=b^2-4ac`

In this case you have the following quadratic equation:

`4x^2+12x+9=0`

Where:

`a=4\\b=12\\c=9`

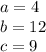
Therefore, when you substitute these values into the formula, you get that the discriminant is this:

`D=(12)^2-4(4)(9)\\\\D=0`

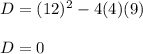
Since
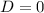`D=0`, the quadratic equation has one real root with a multiplicity of 2 .