Given:
Rate of increase in ripple radius,
 = 2 ft/sec
= 2 ft/sec
Solution:
Area of circle =
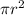
Differentiating w.r.t 'r', we get:
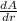 = 2
= 2
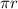
Rate of change in area is given by:
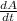 =
=
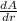 .
.

(by chain rule)
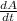 = 2
= 2
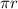 .
.

when radius, r = 5ft
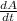 = 2
= 2
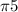 . 2 = 20
. 2 = 20

Now,
when r = 10 ft
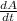 = 2
= 2
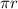 .
.

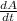 = 2
= 2
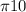 . 2 = 40
. 2 = 40
