Explanation:
(a) Total repairs on an average in 3 years is given by:
2 repairs per year,
so , in 3 years it will be
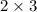 = 6 repairs
= 6 repairs
Now, from Poisson distribution,
P =
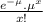 (1)
(1)
where,
 = no. of times an event occurs
= no. of times an event occurs
x = 0, 1, 2, .......
Now, using eqn (1):
P(X = x) =
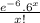
To calculate the probability of less than 2 repairs in the 3 years:
for
![P[X<2]](https://img.qammunity.org/2020/formulas/mathematics/college/1ko0vjdk33as40ejequ8keuamjxvv61d26.png)
Now,
![P[X<2] = P[X = 0] + P[X = 1]](https://img.qammunity.org/2020/formulas/mathematics/college/52k08hfmn4u16lxtvslyi8vwc96aa3yfbo.png)
![P[X<2]](https://img.qammunity.org/2020/formulas/mathematics/college/1ko0vjdk33as40ejequ8keuamjxvv61d26.png) =
=
 +
+
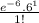
![P[X<2]](https://img.qammunity.org/2020/formulas/mathematics/college/1ko0vjdk33as40ejequ8keuamjxvv61d26.png) = 0.01735
= 0.01735
(b) To calculate the probability for 1 and 2 more years for next repair, if current repairs are 3:
The distribution function can be given by:
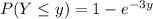 (2)
(2)
Let Y denote the wait for next year and using eqn (2)
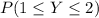 =
=

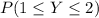 =
=
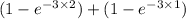
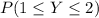 = 0.04731
= 0.04731
Answer:
(a) The probability for less than 2 repairs in next 3 years is 0.01735
(b) The probability to wait between 1 and 2 more years for next repair is 0.04731