Question

Real estate ads suggest that 75 % of homes for sale have​ garages, 29 % have swimming​ pools, and 13 % have both features. What is the probability that a home for sale has ​a) a pool or a​ garage? ​b) neither a pool nor a​ garage? ​c) a pool but no​ garage?

Answer 1

Answer: a) 91% b) 9% c) 16%

Explanation:

Let A be the event that homes for sale have​ garages and B be the event that homes for sale have​ swimming​ pools.

Now, given :
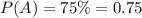
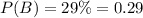
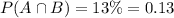
`P(A)=75\%=0.75`

`P(B)=29\%=0.29`

`P(A\cap B)=13\%=0.13`

a)
`P(A\cup B)=P(A)+P(B)-P(A\cap B)\\\\\Rightarrow\ P(A\cup B)=0.75+0.29-0.13=0.91`

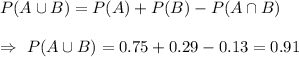
Hence, the probability that a home for sale has a pool or a​ garage is 91%.

b) The probability that a home for sale has ​neither a pool nor a​ garage is given by :-

`1-P(A\cup B)=1-0.91=0.09`

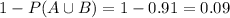
Hence, the probability that a home for sale has ​neither a pool nor a​ garage is 9%.

c) The probability that a home for sale has a pool but no​ garage is given by :-

`P(B)-P(A\cap B)=0.29-0.13=0.16`

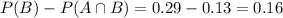
Hence, the probability that a home for sale has a pool but no​ garage is 16%.