Question

Suppose a study finds that the wing lengths of houseflies are normally distributed with a mean of 4.55mm and a standard deviation of about 0.392mm. What is the probability that a randomly selected housefly has a wing length between 4mm and 5mm?

Answer 1

Answer: 0.7941

Step-by-step explanation:

Given : Suppose a study finds that the wing lengths of houseflies are normally distributed with mean :
`\mu=4.55\text{ mm}`

`\sigma=0.392\text{ mm}`

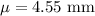
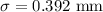
Let X be the random variable that represents the wing lengths of a randomly selected housefly.

Z-score :
`z=(x-\mu)/(\sigma)`

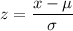
For x = 4 mm

`z=(4-4.55)/(0.392)\approx-1.40`

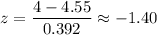
For x = 5 mm

`z=(5-4.55)/(0.392)\approx1.15`

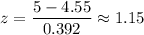
Now, the probability that a randomly selected housefly has a wing length between 4mm and 5mm is given by :-

`P(4<X<5)=P(-1.4<z<1.15)\\\\P(1.15)-P(-1.4)=0.8749281-0.0807567\\\\=0.7941714\approx0.7941`

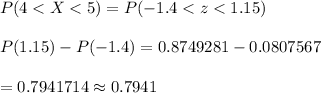
Hence, the probability that a randomly selected housefly has a wing length between 4mm and 5mm is 0.7941 .