Question

The rate constant for this first‑order reaction is 0.150 s−1 at 400 ∘C. A⟶products How long, in seconds, would it take for the concentration of A to decrease from 0.860 M to 0.260 M?

Answer 1

To determine the time for the concentration of substance A to decrease in a first-order reaction, the formula t = (1/k) * ln([A]0/[A]t) is used with the known rate constant and initial and final concentrations.

Step-by-step explanation:

The question asks how long it would take for the concentration of substance A to decrease from 0.860 M to 0.260 M given a first-order reaction with a rate constant of 0.150 s−¹ at 400 °C.

For a first-order reaction, the time (t) it takes for the concentration of a reactant to change can be found using the formula:

t = (1/k) * ln([A]0/[A]t)

Where:

• t = Time
• k = Rate constant
• [A]0 = Initial concentration of A
• [A]t = Final concentration of A

In this case, we can substitute the given values into the equation:

t = (1/0.150 s−¹) * ln(0.860 M / 0.260 M) = (1/0.150 s−¹) * ln(3.3077)

The time can be calculated by completing the computation for ln(3.3077) and dividing by the rate constant.

Answer 2

Answer : The time taken for the concentration will be, 7.98 seconds

Explanation :

First order reaction : A reaction is said to be of first order if the rate is depend on the concentration of the reactants, that means the rate depends linearly on one reactant concentration.

Expression for rate law for first order kinetics is given by :

`k=(2.303)/(t)\log([A]_o)/([A])`

where,

k = rate constant =
`0.150s^(-1)`

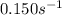
t = time taken for the process = ?

`[A]_o` = initial concentration = 0.860 M

`[A]` = concentration after time 't' = 0.260 M

Now put all the given values in above equation, we get:

`0.150s^(-1)=(2.303)/(t)\log(0.860)/(0.260)`

`t=7.98s`

Therefore, the time taken for the concentration will be, 7.98 seconds