Question

The weights of steers in a herd are distributed normally. The standard deviation is 300lbs and the mean steer weight is 1100lbs. Find the probability that the weight of a randomly selected steer is greater than 920lbs. Round your answer to four decimal places.

Answer 1

Answer: 0.7257

Explanation:

Given : The weights of steers in a herd are distributed normally.

`\mu= 1100\text{ lbs }`

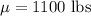
Standard deviation :
`\sigma=300 \text{ lbs }`

Let x be the weight of the randomly selected steer .

Z-score :
`(x-\mu)/(\sigma)`

`z=(920-1100)/(300)=-0.6`

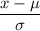
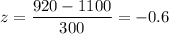
The the probability that the weight of a randomly selected steer is greater than 920 lbs using standardized normal distribution table :

`P(x>920)=P(z>-0.6)=1-P(z<-0.6)\\\\=1-0.2742531=0.7257469\approx0.7257`

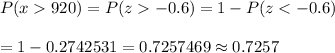
Hence, the probability that the weight of a randomly selected steer is greater than 920lbs =0.7257