Question

An electron moving at right angles to a 0.1 T magnetic field experiences an acceleration of 6 × 1015 m.s-2. What is the speed of the electron? How much does its speed change in 1 ns (10-9 s)?

Answer 1

Step-by-step explanation:

It is given that,

Magnetic field, B = 0.1 T

Acceleration,
`a=6* 10^(15)\ m/s^2`

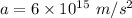
Charge on electron,
`q=1.6* 10^(-19)\ C`

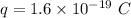
Mass of electron,
`m=9.1* 10^(-31)\ kg`

(a) The force acting on the electron when it is accelerated is, F = ma

The force acting on the electron when it is in magnetic field,
`F=qvB\ sin\theta`

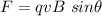
Here,
`\theta=90`

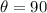
So,
`ma=qvB`

Where

v is the velocity of the electron

B is the magnetic field

`v=(ma)/(qB)`

`v=(9.1* 10^(-31)\ kg* 6* 10^(15)\ m/s^2)/(1.6* 10^(-19)\ C* 0.1\ T)`

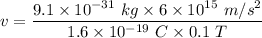
v = 341250 m/s

or

`v=3.41* 10^5\ m/s`

So, the speed of the electron is
`3.41* 10^5\ m/s`

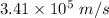
(b) In 1 ns, the speed of the electron remains the same as the force is perpendicular to the cross product of velocity and the magnetic field.