Solution:
Given:
a(t) = 18t + 4
at t = 0 :
s(0) = 8
v(0) = 7
where,
s = position of particle
v = velocity of particle
Now, we know the following relations:
a =
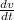
v = ∫a dt = ∫(18t + 4)dt = 9
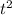 + 4t + C
+ 4t + C
at t = 0 :
v(0) = 9(0) +4(0) + C
⇒ C = v(0) = 7
⇒ v (t) = 9
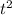 + 4t +7
+ 4t +7
Now, using the relation:
v =
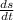
s = ∫v dt = ∫(9
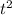 + 4t +7)dt = 3
+ 4t +7)dt = 3
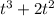 + 7t + C
+ 7t + C
at t = 0 :
s(0) = 3(0) + 2(0) + 7(0) + C
⇒ C = s(0) = 8
⇒ s(t) = 3
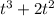 + 7t + 8
+ 7t + 8
Now, position at t = 5 :
s(5) = 3
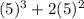 + 7(5) + 8
+ 7(5) + 8
s = 468