Question

Could use some help with this question please!

Answer 1

so we know the angle is 180° < x < 270°, which is another way of saying that the angle is in III Quadrant, where cosine as well as sine are both negative, which as well means a positive tangent, recall tangent = sine/cosine.

the cos(x) = -(4/5), now, let's recall that the hypotenuse is never negative, since it's just a radius unit, thus

`\bf cos(x)=\cfrac{\stackrel{adjacent}{-4}}{\stackrel{hypotenuse}{5}}\qquad \impliedby \textit{let's find the \underline{opposite side}} \\\\\\ \textit{using the pythagorean theorem} \\\\ c^2=a^2+b^2\implies \pm √(c^2-a^2)=b \qquad \begin{cases} c=hypotenuse\\ a=adjacent\\ b=opposite\\ \end{cases} \\\\\\ \pm√(5^2-(-4)^2)=b\implies \pm√(9)=b\implies \pm 3 = b\implies \stackrel{III~Quadrant}{\boxed{-3=b}} \\\\[-0.35em] ~\dotfill`

`\bf tan(x)=\cfrac{\stackrel{opposite}{-3}}{\stackrel{adjacent}{-4}}\implies tan(x)=\cfrac{3}{4} \\\\\\ tan(2x)=\cfrac{2tan(x)}{1-tan^2(x)}\implies tan(2x)=\cfrac{2\left( (3)/(4) \right)}{1-\left( (3)/(4) \right)^2}\implies tan(2x)=\cfrac{~~(3)/(2)~~}{1-(9)/(16)}`

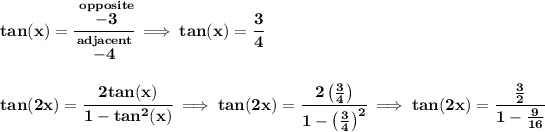
`\bf tan(2x)=\cfrac{~~(3)/(2)~~}{(16-9)/(16)}\implies tan(2x)=\cfrac{~~(3)/(2)~~}{(7)/(16)}\implies tan(2x)=\cfrac{3}{~~\begin{matrix} 2 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}\cdot \cfrac{\stackrel{8}{~~\begin{matrix} 16 \\[-0.7em]\cline{1-1}\\[-5pt]\end{matrix}~~}}{7} \\\\\\ tan(2x)=\cfrac{24}{7}\implies tan(2x)=3(3)/(7)`