Answer: 21
Explanation:
Given : The scores on the midterm exam are normally distributed with

Let X be random variable that represents the score of the students.
z-score:

For x=82
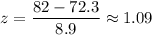
For x=90
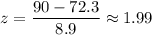
Now, the probability of the students in the class receive a score between 82 and 90 ( by using standard normal distribution table ) :-

Now ,the number of students expected to receive a score between 82 and 90 are :-

Hence, 21 students are expected to receive a score between 82 and 90 .