Question

Rationalize the denominator and simplify.

Answer 1

let's use the conjugate of the denominator and multiply top and bottom by it, recall the conjugate of a binomial is simply the same binomial with a different sign in between.

`\bf \cfrac{2√(x)-3√(y)}{√(x)+√(y)}\cdot \cfrac{√(x)-√(y)}{√(x)-√(y)}\implies \cfrac{2√(x)√(x)-2√(x)√(y)~~-~~3√(x)√(y)+3√(y)√(y)}{\underset{\textit{difference of squares}}{(√(x)+√(y))(√(x)-√(y))}} \\\\\\ \cfrac{2√(x^2)-2√(xy)-3√(xy)+3√(y^2)}{(√(x))^2-(√(y))^2}\implies \cfrac{2x-5√(xy)+3y}{x-y}`

Answer 2

`(2x-5√(xy)+3y)/(x-y)\\`

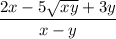
Explanation:

In Rationalize the denominator we multiply both numerator and denominator by the conjugate of denominator.

In Conjugate we change the sign of middle operator.

Example: Congugate of (a + b) = a - b

Now Solving the given expression,

`(2√(x) - 3√(y))/(√(x) + √(y)) = (2√(x) - 3√(y))/(√(x) + √(y))* (√(x) - √(y))/(√(x) - √(y))\\\\\Rightarrow \frac{(2√(x) - 3√(y))(√(x) - √(y))}{( √(x) + √(y)){(√(x) - √(y)})}\ \ \ \ \ \ \ \ \ \ \ [\because (a-b)(a+b)=(a^(2) +b^(2))]\\\Rightarrow (2x-2√(xy)-3√(xy)+3y)/(x-y)\\\\ \Rightarrow (2x-5√(xy)+3y)/(x-y)\\`