Answer:
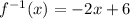 .
.
Explanation:
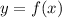

The biggest thing about finding the inverse is swapping x and y. The inverse comes from switching all the points on the graph of the original. So a point (x,y) on the original becomes (y,x) on the original's inverse.
Sway x and y in:

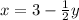
Now we want to remake y the subject (that is solve for y):
Subtract 3 on both sides:
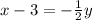
Multiply both sides by -2:
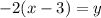
We could leave as this or we could distribute:
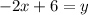
The inverse equations is
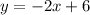 .
.
Now some people rename this
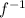 or just call it another name like
or just call it another name like
 .
.
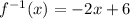 .
.
Let's verify this is the inverse.
If they are inverses then you will have that:
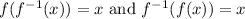
Let's try the first:
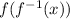
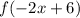 (Replace inverse f with -2x+6 since we had
(Replace inverse f with -2x+6 since we had
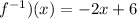
 (Replace old output, x, in f with new input, -2x+6)
(Replace old output, x, in f with new input, -2x+6)
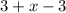 (I distributed)
(I distributed)

Bingo!
Let's try the other way.
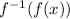
 (Replace f(x) with 3-(1/2)x since
(Replace f(x) with 3-(1/2)x since
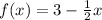 )
)
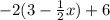 (Replace old input, x, in -2x+6 with 3-(1/2)x since
(Replace old input, x, in -2x+6 with 3-(1/2)x since
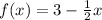 )
)
 (I distributed)
(I distributed)

So both ways we got x.
We have confirmed what we found is the inverse of the original function.