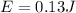Question

A 13.0-Ω resistor, 13.5-mH inductor, and 50.0-µF capacitor are connected in series to a 55.0-V (rms) source having variable frequency. If the operating frequency is twice the resonance frequency, find the energy delivered to the circuit during one period.

Answer 1

E = 0.13 J

Step-by-step explanation:

At resonance condition we have

`\omega = \sqrt{(1)/(LC)}`

`\omega = \sqrt{(1)/((13.5 * 10^(-3)){50* 10^(-6))}}`

`\omega = 1217.2 rad/s`

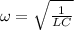
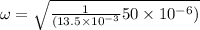
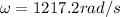
now if the frequency is double that of resonance condition then we have

`x_L = 2\omega L`

`x_L = 2(1217.2)(13.5* 10^(-3))`

`x_L = 32.86 ohm`

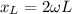
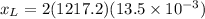
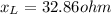
now we have

`x_c = (1)/(2(1217)(50* 10^(-6)))`

`x_c = 8.22 ohm`

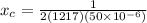
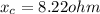
now average power is given as

`P = i_(rms)V_(rms)* (R)/(z)`

`P = (55)/(√((32.86 - 8.22)^2 + 13^2)))(55)* (13)/(√((32.86 - 8.22)^2 + 13^2))`

`P_(avg) = 50.67 Watt`

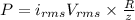
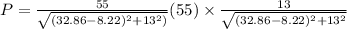
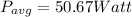
Now time period is given as

`T = (2\pi)/(\omega)`

so total energy consumed is given as

`E_(avg) = 50.67((2\pi)/(2(1217.2)))`

`E = 0.13 J`