Answer:
The bond will decrease by:
$27.019642
Their market value will be:
$972.980358
Step-by-step explanation:
The price of the bond will decrease in order to increase the yield of the bond to 9.10%
We will calculate the present value of the annuity using the 9.10 rate compounding semiannually
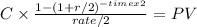
c= 1000 x 8.75%/2 = 1000 x 0.0875/2 = 43.75
time = 25 years - 3 = 22 years
rate 9.10% = 0.091
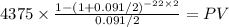
PV = 825.798092
Then we calculate the present value of the redem of the bond:
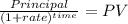
Face value = 1,000
rate = 0.091
time = 22
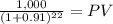
PV = 147,182266
We add both to get the current PV at the new yield to maturity
825.798092 + 147,182266 = 972.980358
1000 - 972.980358 = ↓27.019642