Question

I need help with this problem.
​

Answer 1

(1, 4)

Explanation:

You must specify the domain of the function.

We know: There is no square root of the negative number.

Therefore

x - 1 ≥ 0 add 1 to both sides

x ≥ 1

The first argument for which the function exists is the number 1.

We will calculate the function value for x = 1.

Put x = 1 to the equation of the function:

`y=-√(1-1)+4=-\sqrt0+4=0+4=4`

Therefore the starting point of the graph of given function is (1, 4).

Answer 2

(1,4)

Explanation:

Let's this of
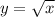`y=√(x)` which is it's parent function.

How do we get to
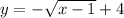`y=-√(x-1)+4` from there?

It has been reflected about the a-axis because of the - in front of the square root.

It has been shifted right 1 unit because of the -(1) in the square root.

It has been moved up 4 units because of the +4 outside the square root.

In general:

`y=a(x-h)^2+k` has the following transformations from the parent:

Moved right h units if h is positive.

Moved left h units if h is negative.

Moved up k units if k is positive.

Moved down k units if k is negative.

If
`a` is positive, it has not been reflected.

If
`a` is negative, it has been reflected about the x-axis.

`a` also tells us about the stretching factor.

The parent function has a starting point at (0,0). Where does this point move on the new graph?

It new graphed was the parent function but reflected over x-axis and shifted right 1 unit and moved up 4 units.

So the new starting point is (0+1,0+4)=(1,4).