Question

The volume of a cantaloupe is approximated by Upper V equals four thirds pi font size decreased by 5 r cubedV= 4 3π r3. The radius is growing at the rate of 0.5 cm divided by week0.5 cm/week​, at a time when the radius is 5.85.8 cm. How fast is the volume changing at that​ moment?

Answer 1

68.445 cm³/s

Step-by-step explanation:

Given:

Volume, V =
`(4)/(3)\pi r^3`

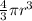
radius = 5.85 cm

Growth rate of radius = 0.5 cm/week

now

differentiating the volume with respect to time 't', we get:

`(dV)/(dt)=(d((4)/(3)\pi r^3))/(dt)`

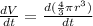
or

`(dV)/(dt)=((4)/(3)\pi )3r^2(dr)/(dt)`

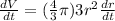
now, substituting the value of r (i.e at r = 5.85cm) in the above equation, we get:

`(dV)/(dt)=4\pi 5.85^2* 0.5`

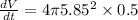
or

`(dV)/(dt)=68.445cm^3/s`

hence, the rate of change of volume at r = 5.85cm is 68.445 cm³/s