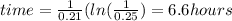Answer:
It will take 6.6 hours for 75% of the lead to decay.
Step-by-step explanation:
The radioactive decay follows first order rate law
The half life and rate constant are related as

The rate law for first order reaction is
![time=(1)/(k)(ln[(A_(0))/(A_(t))]](https://img.qammunity.org/2020/formulas/chemistry/college/558d6sqt154r3qbcwg39s832ggr7ssu565.png)
Where
A0 = initial concentration = 1 g
At= final concentration = 0.25 g (as 75% undergoes decay so 25% left]