Answer: 0.5848
Explanation:
The formula of probability for Poisson distribution for random variable x :-
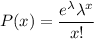 , where
, where
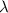 is the mean of the distribution .
is the mean of the distribution .
Given : The auto parts department of an automotive dealership sends out a mean of 3.3 special orders daily.
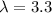
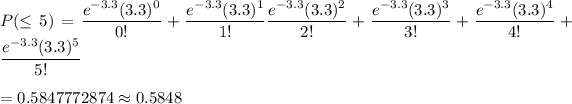
Hence, the probability that, for any day, the number of special orders sent out will be no more than 5 = 0.5848