Question

A 1.00 kg object is attached to a horizontal spring. The spring is initially stretched by 0.400 m, and the object is released from rest there. It proceeds to move without friction. The next time the speed of the object is zero is 0.200 s later. What is the maximum speed of the object?

Answer 1

v = 6.283 m/s

Step-by-step explanation:

Given:

mass of the object, m = 1.00kg

The next time the speed is zero is at t = 0.200s i.e the one half of a total oscillation.

thus,

The time (T) for one complete oscillation will be = 2 × 0.200s = 0.4s

Now,

we know time period (T) is given as:

`T=2\pi \sqrt(m)/(k)`

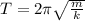
where, k is the spring constant

substituting the values in the above equation we get

`0.4=2\pi \sqrt(1)/(k)`

or

`(m)/(k) = ((0.4)/(2\pi))^2`

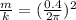
or

k = 246.70 N/m

Then, using the concept of conservation of energy, we have

`(1)/(2)kx^2=(1)/(2)mv^2`

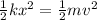
where,

x is the displacement in the spring

v = speed of the object

substituting the values in the above equation we get

`(1)/(2)246.70* 0.400^2=(1)/(2)1* v^2`

or

`19.73* 2= v^2`

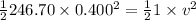
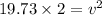
or

v = 6.283 m/s (Answer)