Question

0.5000 kg of water at 35.00 degrees Celsius is cooled, with the removal of 6.300 E4 J of heat. What is the final temperature of the water? Specific heat capacity of water is 4186 J/(kg Co).Remember to identity all of your data, write the equation, and show your work.

Answer 1

Answer : The final temperature of the water is
`65.10^oC`

Explanation :

Formula used :

`q=m* c* (T_(final)-T_(initial))`

where,

q = heat released =
`6.300* 10^(4)J`

m = mass of water = 0.5000 kg

c = specific heat of water =
`4186J/kg^oC`

`T_(final)` = final temperature = ?

`T_(initial)` = initial temperature =
`35.00^oC`

Now put all the given values in the above formula, we get:

`6.300* 10^(4)J=(0.5000kg)* (4186J/kg^oC)* (T_(final)-35.00)^oC`

`T_(final)=65.10^oC`

Therefore, the final temperature of the water is
`65.10^oC`

Answer 2

65.1 °C

Step-by-step explanation:

m = mass of the water = 0.5 kg

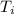`T_(i)` = initial temperature of water = 35.00 °C

`T_(f)` = final temperature of water

c = specific heat of water = 4186 J/(kg °C)

Q = Amount of heat removed from water = 6.3 x 10⁴ J

Amount of heat removed from water is given as

Q = m c (
`T_(f)` -
`T_(i)`)

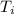Inserting the values

6.3 x 10⁴ = (0.5) (4186) (
`T_(f)` - 35.00)

`T_(f)` = 65.1 °C