Answer:
1.5 x 10¹⁴
Step-by-step explanation:
For the nucleus :
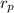 = radius of proton = 1.0 x 10⁻¹⁵ m
= radius of proton = 1.0 x 10⁻¹⁵ m
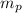 = mass of proton = 1.67 x 10⁻²⁷ kg
= mass of proton = 1.67 x 10⁻²⁷ kg
density of nucleus is given as
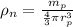

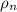 = 3.98 x 10¹⁷
= 3.98 x 10¹⁷
For the atom :
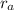 = radius of atom = radius of proton + radius of orbit = (1.0 x 10⁻¹⁵ + 5.3 x 10⁻¹¹) m
= radius of atom = radius of proton + radius of orbit = (1.0 x 10⁻¹⁵ + 5.3 x 10⁻¹¹) m
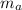 = mass of atom = mass of proton + mass of electron = 1.67 x 10⁻²⁷ + 9.31 x 10⁻³¹ kg
= mass of atom = mass of proton + mass of electron = 1.67 x 10⁻²⁷ + 9.31 x 10⁻³¹ kg
density of atom is given as
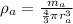
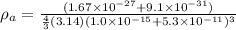
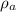 = 2680.5
= 2680.5
Ratio is given as
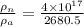
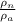 = 1.5 x 10¹⁴
= 1.5 x 10¹⁴