Question

Calculate Δ Hrxn for the following reaction: CH4(g)+4Cl2(g)→CCl4(g)+4HCl(g) given these reactions and their ΔH values: C(s)C(s)H2(g)+++2H2(g)2Cl2(g)Cl2(g)→→→CH4(g),CCl4(g),2HCl(g),ΔH=−74.6 kJΔH=−95.7 kJΔH=−184.6 kJ Express the enthalpy in kilojoules to one decimal place.

Answer 1

-390.3 KJ

Step-by-step explanation:

For Hess's Law, we need to get the corresponding equation below using the sequence of reactions given

By manipulating the reaction, either reversing them or multiplying/dividing them to a certain factor, we can get to the target equation as well as the total enthalpy

CH4(g) + 4Cl2(g) → CCl4(g) + 4HCl(g)

C(s) + 2H2(g) → CH4(g) ΔH = −74.6kJ (needs to reverse)

C(s) + 2Cl2(g) → CCl4(g) ΔH = −95.7kJ (retain)

H2(g) + Cl2(g) → 2HCl(g) ΔH = −184.6kJ (multiply by 2 to get 4Cl2 and cancel out 4 HCl and 4 H2)

Therefore, it is -390.3 KJ

Answer 2

Answer : The enthalpy of the following reaction is, -390.3 KJ

Explanation :

The given balanced chemical reactions are,

(1)
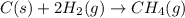
`C(s)+2H_2(g)\rightarrow CH_4(g)`
`\Delta H_1=-74.6KJ/mole`

(2)
`C(s)+2Cl_2(g)\rightarrow CCl_4(g)`
`\Delta H_2=-95.7KJ/mole`

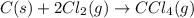
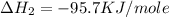
(3)
`H_2(g)+Cl_2(g)\rightarrow 2HCl(g)`
`\Delta H_3=-184.6KJ/mole`

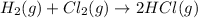
The final reaction of is,

`CH_4(g)+4Cl_2(g)\rightarrow CCl_4(g)+4HCl(g)`
`\Delta H_(rxn)=?`

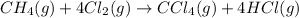
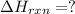
Now adding reaction 2 and twice of reaction 3 and reverse of reaction 1, we get the enthalpy of of the reaction.

The expression for enthalpy for the following reaction will be,

`\Delta H_(rxn)=[2* \Delta H_3]+[-1* \Delta H_1]+[1* \Delta H_2]`

where,

n = number of moles

Now put all the given values in the above expression, we get:

`\Delta H_(rxn)=[2mole* (-184.6KJ/mole)]+[-1mole* (-74.6KJ/mole)]+[1* (-95.7KJ/mole)]=-390.3KJ`

Therefore, the enthalpy of the following reaction is, -390.3 KJ