Answer : The total pressure in the container at equilibrium is, 0.4667 atm
Solution : Given,
Initial pressure of
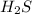 = 0.259 atm
= 0.259 atm
Equilibrium constant,
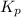 = 0.841
= 0.841
The given equilibrium reaction is,
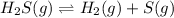
Initially 0.259 0 0
At equilibrium (0.259 - x) x x
Let the partial pressure of
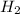 and
and
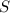 will be, 'x'
will be, 'x'
The expression of
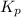 will be,
will be,
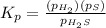
Now put all the values of partial pressure, we get
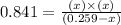
By solving the term x, we get
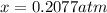
The partial pressure of
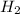 and
and
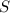 = x = 0.2077 atm
= x = 0.2077 atm
Total pressure in the container at equilibrium =
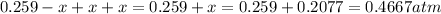
Therefore, the total pressure in the container at equilibrium is, 0.4667 atm