Answer:
Area of triangle is 9.88 units^2
Explanation:
We need to find the area of triangle
Given E(5,1), F(0,4), D(0,8)
We will use formula:
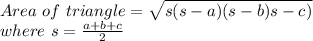
We need to find the lengths of side DE, EF and FD
Length of side DE = a =
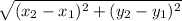
Length of side DE = a =
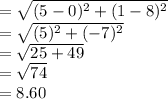
Length of side EF = b =
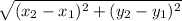
Length of side EF = b =
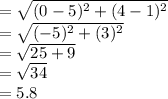
Length of side FD = c =
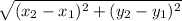
Length of side FD = c =
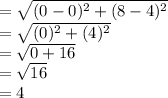
so, a= 8.60, b= 5.8 and c = 4
s = a+b+c/2
s= 8.6+5.8+4/2
s= 9.2
Area of triangle=
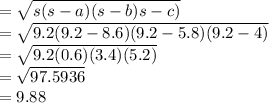
So, area of triangle is 9.88 units^2