Answer:
The focal length of the eyepiece is 4.012 cm.
Step-by-step explanation:
Given that,
Focal length = 1.5 cm
angular magnification = -58
Distance of image = 18 cm
We need to calculate the focal length of the eyepiece
Using formula of angular magnification
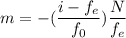
Where,
 = distance between the lenses in a compound microscope
= distance between the lenses in a compound microscope
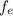 =focal length of eyepiece
=focal length of eyepiece
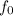 =focal length of the object
=focal length of the object
N = normal point
Put the value into the formula
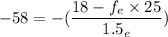
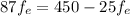
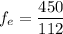
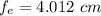
Hence, The focal length of the eyepiece is 4.012 cm.