Question

Misaka solved the radical equation x – 3 = square root of 4x-7 but did not check her solutions. (x – 3)2 = square root of 4x-7^2 x2 – 6x + 9 = 4x – 7 x2 – 10x + 16 = 0 (x – 2)(x – 8) = 0 x = 2 and x = 8 Which shows the true solution(s) to the radical equation x – 3 = square root of 4x-7 x = 2 x = 8 x = 2 and x = 8 There are no true solutions to the equation.

Answer 1

x=8 is a true solution of the radical equation

Explanation:

we have

`x-3=√(4x-7)`

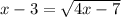
Solve for x

squared both sides

`(x-3)^(2)=4x-7\\\\x^(2)-6x+9=4x-7\\\\ x^(2)-10x+16=0`

Convert to factored form

`x^(2)-10x+16=(x-2)(x-8)`

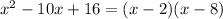
The solutions are x=2 and x=8

Verify the solutions

For x=2

Substitute in the original equation

`2-3=√(4(2)-7)`

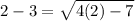
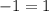`-1=1` ----> is not true

therefore

x=2 is not a true solution of the radical equation

For x=8

Substitute in the original equation

`8-3=√(4(8)-7)`

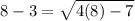
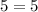`5=5` ----> is true

therefore

x=8 is a true solution of the radical equation