Question

A pressure cylinder has a diameter of 150-mm and has a 6-mm wall thickness. What pressure can this vessel carry if the maximum shear stress is not to exceed 25 MPa?

Answer 1

p = 8N/mm2

Step-by-step explanation:

given data ;

diameter of cylinder = 150 mm

thickness of cylinder = 6 mm

maximum shear stress = 25 MPa

we know that

hoop stress is given as =
`(pd)/(2t)`

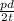
axial stress is given as =
`(pd)/(4t)`

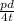
maximum shear stress = (hoop stress - axial stress)/2

putting both stress value to get required pressure

`25 = ( (pd)/(2t) -(pd)/(4t))/(2)`

`25 = (pd)/(8t)`

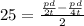
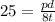
t = 6 mm

d = 150 mm

therefore we have pressure

p = 8N/mm2