Answer:
Tangential Speed equals 5.57m/s
Step-by-step explanation:
In the figure shown for equilibrium along y- axis we have
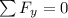
Resolving Forces along y axis we have
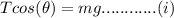
Similarly along x axis
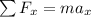
 )/(r)](https://img.qammunity.org/2020/formulas/physics/college/620bt36g95tlc46fjc5bs0vhhyzkcf5hg3.png) ............(ii)[/tex]
............(ii)[/tex]
Dividing ii by i we have
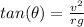
In the figure below we have
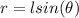
Thus solving for v we have

Applying values we get
v=5.576m/s