Question

In a survey of adults who follow more than one sport, 30% listed football as their favorite sport. You survey 15 adults who follow more than one sport. What is the probability rounded to the nearest tenth that fewer than 4 of them will say that football is their favorite sport?

Answer 1

Answer: 0.5

Explanation:

Binomial probability formula :-

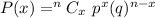`P(x)=^nC_x\ p^x(q)^(n-x)`, where P(x) is the probability of getting success in x trials , n is the total trials and p is the probability of getting success in each trial.

Given : The probability that the adults follow more than one game = 0.30

Then , q= 1-p = 1-0.30=0.70

The number of adults surveyed : n= 15

Let X be represents the adults who follow more than one sport.

Then , the probability that fewer than 4 of them will say that football is their favorite sport,

`P(X\leq4)=P(x=0)+P(x=1)+P(x=2)+P(x=3)+P(x=4)\\\\=^(15)C_(0)\ (0.30)^0(0.70)^(15)+^(15)C_(1)\ (0.30)^1(0.70)^(14)+^(15)C_(2)\ (0.30)^2(0.70)^(13)+^(15)C_(3)\ (0.30)^3(0.70)^(12)+^(15)C_(4)\ (0.30)^4(0.70)^(11)\\\\=(0.30)^0(0.70)^(15)+15(0.30)^1(0.70)^(14)+105(0.30)^2(0.70)^(13)+455(0.30)^3(0.70)^(12)+1365(0.30)^4(0.70)^(11)\\\\=0.515491059227\approx0.5`

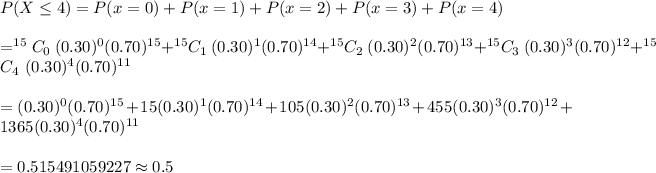
Hence, the probability rounded to the nearest tenth that fewer than 4 of them will say that football is their favorite sport =0.5