Question

A force of 68 Newtons is applied to a wire with a diameter of 0.7 mm. What is the tensile stress (in N/m2) in the wire? Do not include units with the answer.

Answer 1

Given:

Applied Force on wire = 68 N

Diameter of wire, d = 0.7 mm =
`0.7* 10^(-3)` m

Radius of wire, r =
`(d)/(2)` = 0.35 mm =
`0.35* 10^(-3)` m

Formula used:

Stress =
`(Applied Force)/(cross-sectional area)`

Step-by-step explanation:

Cross-sectional area, A =
`\pi r^(2)` =
`\pi (0.35* 10^(-3))^(2)`

A =
`3.84* 10^(-7) m^(2)`

Using the formula for stress:

Stress =
`(68)/(3.84* 10^(-7))` =
`1.76* 10^(8)`

Answer 2

7.07 x 10⁸ N/m²

Step-by-step explanation:

F = Force applied to the wire = 68 N

d = diameter of the wire = 0.7 mm = 0.7 x 10⁻³ m

r = radius of the wire = (0.5) d = (0.5) (0.7 x 10⁻³) = 0.35 x 10⁻³ m

Area of cross-section of wire is given as

A = (0.25) πr²

A = (0.25) (3.14) (0.35 x 10⁻³)²

A = 9.61625 x 10⁻⁸ m²

Tensile stress is given as

`P = (F)/(A)`

`P = (68)/(9.61625* 10^(-8))`

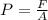
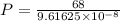
P = 7.07 x 10⁸ N/m²